Cyclic polytope
In mathematics, a cyclic polytope, denoted C(n,d), is a convex polytope formed as a convex hull of n distinct points on a rational normal curve in Rd, where n is greater than d. These polytopes were studied by Constantin Carathéodory, David Gale, Theodore Motzkin, Victor Klee, and others. They play an important role in polyhedral combinatorics: according to the Upper Bound Conjecture, proved by Peter McMullen and Richard Stanley, the boundary Δ(n,d) of the cyclic polytope C(n,d) maximizes the number fi of i-dimensional faces among all simplicial spheres of dimension d − 1 with n vertices.
Contents |
Definition
The moment curve in 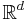 is defined by
is defined by
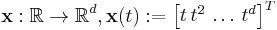 .
.
The  -dimensional cyclic polytope with
-dimensional cyclic polytope with  vertices is the convex hull
vertices is the convex hull
of 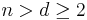 distinct points
distinct points 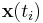 with
with 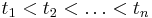 on the moment curve.
on the moment curve.
The combinatorial structure of this polytope is independent of the points chosen, and the resulting polytope has dimension d and n vertices. Its boundary is a (d − 1)-dimensional simplicial polytope denoted Δ(n,d).
Gale evenness condition
The Gale evenness condition [1] provides a necessary and sufficient condition to determine a facet on a cyclic polytope.
Let 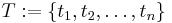 . Then, a
. Then, a  -subset
-subset 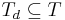 forms a facet of
forms a facet of 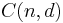 iff any two elements in
iff any two elements in 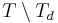 are separated by an even number of elements from
are separated by an even number of elements from 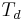 in the sequence
in the sequence 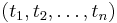 .
.
The upper bound conjecture
The number of i-dimensional faces of Δ(n,d) is given by the formula
and ![(f_0,\ldots,f_{[\frac{d}{2}]-1})](/2012-wikipedia_en_all_nopic_01_2012/I/b120eccf2cea95526573d2ea6546eb0d.png) completely determine
completely determine ![(f_{[\frac{d}{2}]},\ldots,f_{d-1})](/2012-wikipedia_en_all_nopic_01_2012/I/6ffa8cbf0630129a73af6f375db20cb2.png) via the Dehn–Sommerville equations.
via the Dehn–Sommerville equations.
The Upper Bound Conjecture states that if Δ is a simplicial sphere of dimension d − 1 with n vertices , then
The Upper Bound Conjecture for simplicial polytopes was proposed by Motzkin in 1957 and proved by McMullen in 1970. A key ingredient in his proof was the following reformulation in terms of h-vectors:
Victor Klee suggested that the same statement should hold for all simplicial spheres and this was indeed established in 1975 by Stanley [2] using the notion of a Stanley–Reisner ring and homological methods
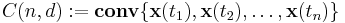
![f_i(\Delta(d,n)) = \binom{n}{i%2B1} \quad \textrm{for} \quad
0 \leq i < \left[\frac{d}{2}\right]](/2012-wikipedia_en_all_nopic_01_2012/I/8db366602bd336d3d23d7bb382f80e67.png)
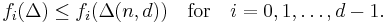
![h_i(\Delta) \leq \tbinom{n-d%2Bi-1}{i} \quad
\textrm{for} \quad
0 \leq i < \left[\frac{d}{2}\right].](/2012-wikipedia_en_all_nopic_01_2012/I/714b949003c56e66987e56cb14f8236c.png)